Koordinatsystemet

Et vigtigt matematisk værktøj er koordinatsystemet.

Et koordinatsystem består af to akser, der står vinkelret på hinanden.

Den vandrette akse kaldes \(x\)-aksen eller førsteaksen. Den lodrette kaldes \(y\)-aksen eller andenaksen.

De to akser skærer hinanden i et punkt, der kaldes origo.

Akserne deler koordinatsystemet ind i fire stykker. Hver af dem kaldes en kvadrant. Kvadranterne er nummereret 1-4 for at skelne mellem dem. 1. kvadrant er oppe til højre, og så nummereres de ellers mod uret.

Punkter

De to akser fungerer som tallinjer. Begge tallinjer er 0 i origo.

\(x\)-aksen er positiv til højre og negativ til venstre for origo.

\(y\)-aksen er positiv ovenfor og negativ nedenunder origo.

Hvis man har et punkt i planen, kan man omtale det ved dets koordinater.

Man finder koordinaterne ved at gå lodret og vandret ind på de to akser. På \(x\)-aksen aflæses \(x\)-koordinatet og på \(y\)-aksen aflæses \(y\)-koordinatet.

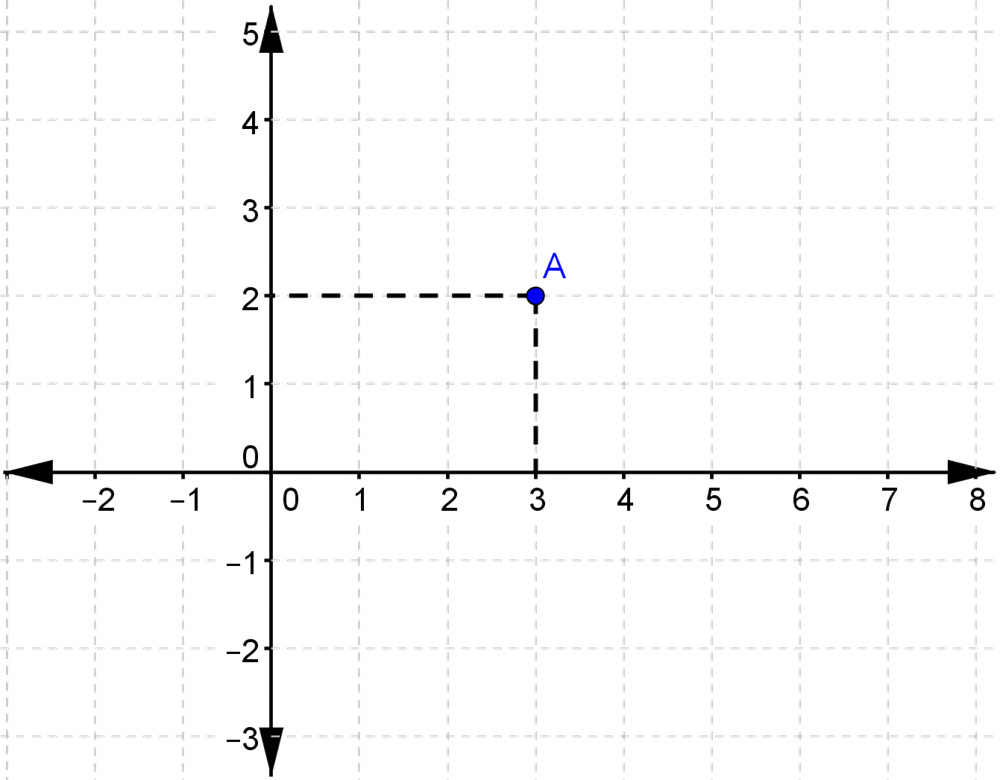
Punktet A har \(x\)-koordinat 3 og \(y\)-koordinat 2.

Man skriver koordinaterne op i en parentes, hvor man først skriver \(x\)-koordinatet, dernæst et komma eller semikolon, og derpå \(y\)-koordinatet.

Punktet \(A\) har dermed koordinaterne (3,2).

Her er indtegnet nogle punkter med koordinater

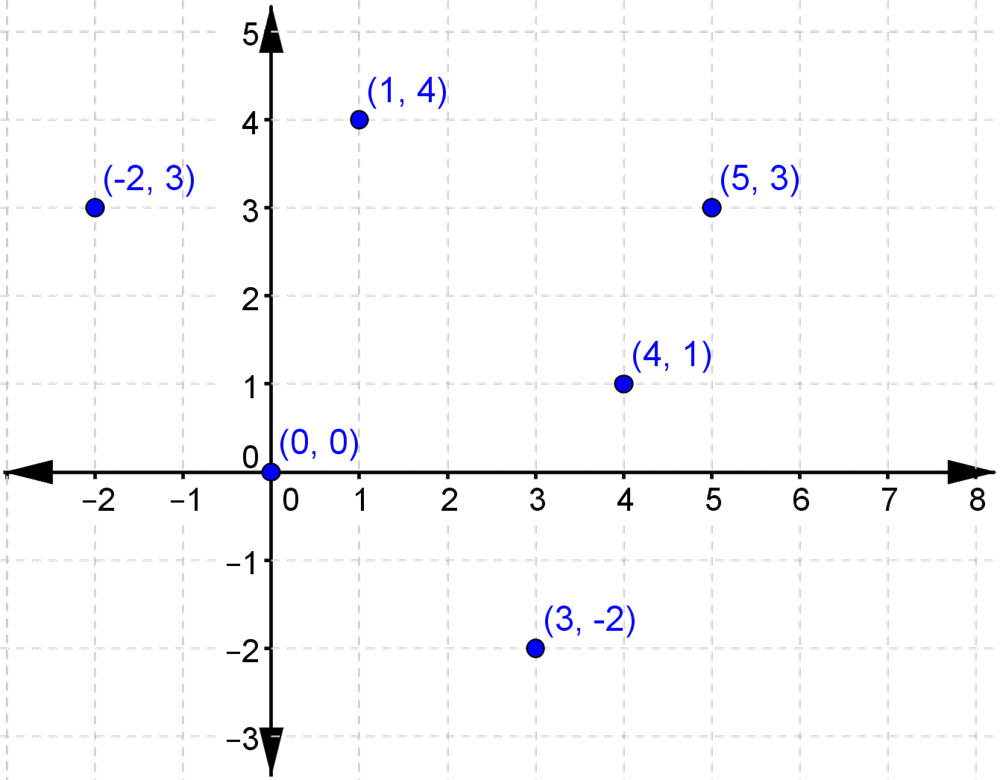
Prøv selv i et koordinatsystem at afsætte punkterne (1,1), (3,4), (2,-1), (5,2) og (-1,-3).