Trekantens tyngdepunkt
Tyngdepunkt for firkanter:
Vi kan først betragte tyngdepunktet for firkanter:
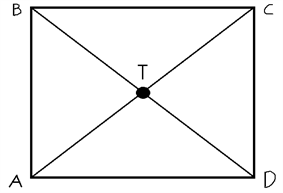
Her er tyngdepunktet, hvor diagonalerne skærer hinanden. Det punkt kalder vi for tyngdepunktet T. (En god regel er, at de dannede trekanter skal alle have samme areal)
Tyngdepunkt for trekanter:
Tyngdepunktet er dér, hvor medianerne skærer hinanden. Her har alle de dannede trekanter også samme areal.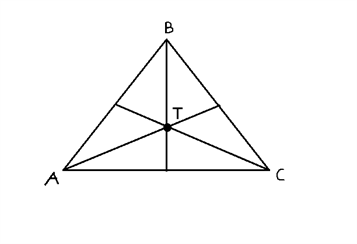 
Vi kan kigge på trekanten i et koordinatsystem:
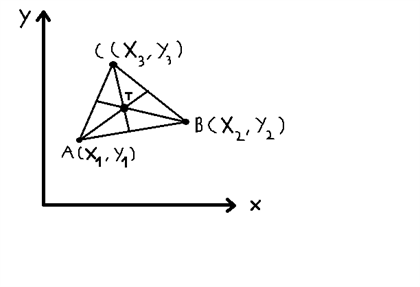Her kan vi skrive tyngdepunktet med formlen: $$T(x,y)=(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})$$
Eksempel 1 - find tyngdepunkt ud fra givet figur:
En trekant ABC er indtegnet i et koordinatsystem:
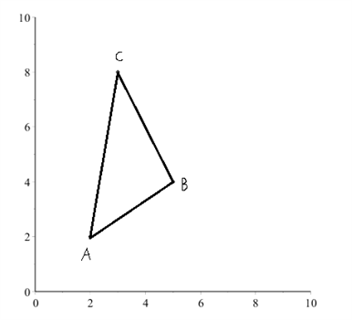
Vi skal finde trekantens tyngdepunkt og indtegne det i trekanten: $$T(x,y)=(\frac{2+5+3}{3},\frac{2+4+8}{3})=(\frac{10}{3},\frac{14}{3})=(3.33,4.66)$$ Tyngdepunkt kan nu indtegnes:
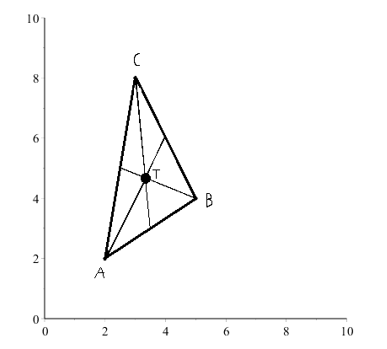
Eksempel 2 - udregne punkt i trekant ud fra to punkter og tyngdepunkt
Vi har fået givet 2 punkter og et tyngdepunkt for en trekant ABC: $$ A=(2,3) \, \, , \, \, B=(7,8) \, \, \, og \, \, \, T(x,y)=(5,4)$$ Vi skal udregne det sidste punkt C som danner en trekant med punkt A og punkt B, hvor trekanten har det oplyste tyngdepunkt. $$T(x,y)=(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})$$ $$(5,4)=(\frac{2+7+x_3}{3},\frac{3+8+y_3}{3})$$
Vi kan nu udregne x-komponenten og y-komponenten hver for sig.
$$5=\frac{9+x_3}{3}\implies x_3=15-9=6$$ $$4=\frac{11+y_3}{3}\implies y_3=12-11=1$$ Dvs. vi nu har punktet C givet ved $$C=(6,1)$$
Industrieksempel - Gaffeltrucks tyngdepunkt vha. stabilitetstrekant
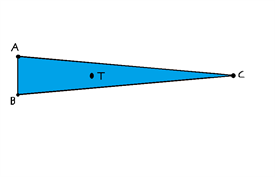
Vi har følgende gaffeltruck, og vi ønsker at finde dens tyngdepunkt:
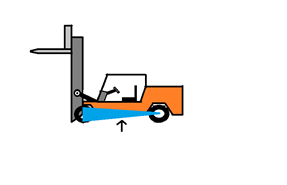Dette kan vi gøre ved at kigge på gaffeltruckens stabilitetstrekant (blå trekant på tegningen).
Denne stabilitetstrekant er meget vigtig, for hvis gaffeltruckens tyngdepunkt ligger uden for stabilitetstrekanten, er gaffeltrucken ustabil og tipper.
Vi kan antage (for dette eksempel), at vi kan beregne gaffeltruckens tyngdepunkt ved brug af vores formel til at finde tyngdepunkter i trekanter.
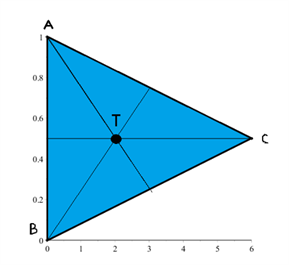
Vi får oplyst, at vi kan betragte de 3 punkter A,B og C i trekanten i et koordinatsystem givet ved:
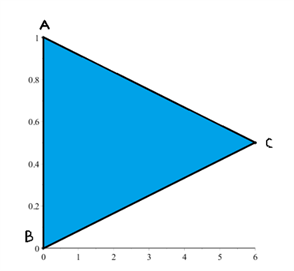
$$T(x,y)=(\frac{0+0+6}{3},\frac{1+0+0.5}{3})=(\, \frac{6}{3},\frac{1.5}{3}\, )=(2,0.5)$$ Vi kan se, at tyngdepunktet T ligger inden for stabilitetstrekanten, og dermed er gaffeltruck stabil.
