Differentiation af funktionen f(x) = ln(x)
Vi ønsker at differentiere funktionen for den naturlige logaritme (med Eulers tal \(e\) som grundtal), \(f(x) = \ln(x), x>0\), dvs. vi vil bestemme \(f’(x)\).
For at bestemme \(f’(x)\) starter vi med at forestille os en sekant, der går gennem to punkter \((x, f(x))\) og \((x+h, f(x+h))\) på grafen for \(f(x)\), hvor \(h\) er en lille tilvækst til x-værdien, se figur 1.
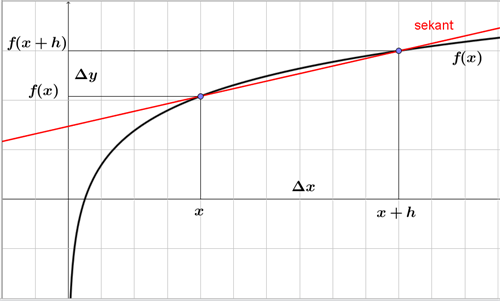
Figur 1 Sekant gennem to punkter på grafen for \(f(x) = \ln(x)\)
Vi opstiller herefter et udtryk for sekantens hældning, \(a_s\):
\(a_s = \dfrac{\Delta y}{\Delta x} = \dfrac{f(x+h) – f(x)}{(x+h) – x} = \dfrac{\ln(x+h) – \ln(x)}{h} = \dfrac{\ln(\frac{x+h}{x})}{h} = \dfrac{\ln(1+\frac{h}{x})}{h}\)
idet vi her har benyttet en af logaritme-regnereglerne, nemlig at logaritmen til en brøk er lig med logaritmen til tælleren minus logaritmen til nævneren.
\(f’(x)\) bestemmer vi herefter som grænseværdien for \(a_s\), når \(h\) bliver uendelig lille, eller udtrykt matematisk:
\(f’(x) = \dfrac{dy}{dx} = \lim_{h\rightarrow 0} a_s = \lim_{h\rightarrow 0} \dfrac{\ln(1+\frac{h}{x})}{h}\)
Frem for at arbejde med en betingelse i grænseværdiudtrykket om, at \(h\rightarrow 0\), vil vi arbejde med betingelsen \(n\rightarrow \infty\). Dette kan vi opnå ved at indføre substitutionen \(h = \frac{1}{n}\), idet betingelsen \(n\rightarrow \infty\) er ensbetydende med, at \(h\rightarrow 0\), og grænseværdibestemmelse af \(f’(x)\) bliver dermed:
\(f’(x) = \lim_{n\rightarrow \infty} \dfrac{\ln(1+\frac{\frac{1}{n}}{x})}{\frac{1}{n}} \implies \dfrac{1}{n}\cdot f’(x) = \ln(1+\dfrac{\frac{1}{x}}{n}), n\rightarrow \infty\)
Hvis vi her beregner \(e\) opløftet til hhv. venstresiden og højresiden og udnytter, at \(e^{\frac{1}{n}\cdot f’(x)} = (e^{f’(x)})^{\frac{1}{n}}\) og at \(e^{\ln(x)} = x\), får vi:
\((e^{f’(x)})^{\frac{1}{n}} = (1 + \dfrac{\frac{1}{x}}{n}), n\rightarrow \infty\).
Idet \(k^{\frac{1}{n}} = \sqrt[n]{k}\) og \((\sqrt[n]{k})^n = k\) kan vi nu opløfte både venstre- og højresiden til den n’te potens og indføre substitutionen \(z = \frac{1}{x}, x>0\) på højresiden:
\(((e^{f’(x)})^{\frac{1}{n}})^n = e^{f’(x)} = (1 + \dfrac{z}{n})^n = (1 + \frac{z}{n})\cdot (1 + \frac{z}{n})\cdot (1 + \frac{z}{n})\cdot ... ... \cdot (1 + \frac{z}{n})\)
hvor højresiden skal forstås som, at det er \(n\) paranteser \((1 + \frac{z}{n})\), der multipliceres, og \(n\rightarrow \infty\).
Vi forestiller os multiplikationen af parenteserne gennemført først med alle \(n\) 1-taller, så med \((n – 1)\) 1-taller og en brøk \(\frac{z}{n}\), derefter med \((n – 2)\) 1-taller og to brøker \(\frac{z}{n}\), osv. Hermed kan vi sammenfatte multiplikationen ved at benytte skrivemåden fra kombinatorikken med \(K_{n,i} = \frac{n!}{i!\cdot (n – i)!}\), hvilket fører til følgende udtryk:
\(e^{f’(x)} = 1 + K_{n,1}\cdot (\frac{z}{n}) + K_{n,2}\cdot (\frac{z}{n})^2 + K_{n,3}\cdot (\frac{z}{n})^3 + ... + K_{n,n-2}\cdot (\frac{z}{n})^{n-2}\)
\(+ K_{n,n-1}\cdot (\frac{z}{n})^{n-1} + (\frac{z}{n})^n\)
\(= 1 + \frac{1}{1!}\cdot \frac{n}{n}\cdot z + \frac{1}{2!}\cdot \frac{n\cdot (n – 1)}{n^2}\cdot z^2 + \frac{1}{3!}\cdot \frac{n\cdot (n – 1)\cdot (n – 2)}{n^3}\cdot z^3 + ... + \frac{1}{2!}\cdot \frac{n\cdot (n – 1)}{n^{n-2}}\cdot z^{n-2}\)
\(+ \frac{1}{1!}\cdot \frac{n}{n^{n-1}}\cdot z^{n-1} + \frac{1}{n^n}\cdot z^n\)
Når \(n\rightarrow \infty\) er højresiden netop rækkeudviklingen af funktionen \(e^z\): \(e^z = e^0 + \frac{1}{1!}\cdot z + \frac{1}{2!}\cdot z^2 + \frac{1}{3!}\cdot z^3 + osv.\)
Hermed når vi frem til:
\(e^{f’(x)} = e^z = e^{\frac{1}{x}}, x>0\)
For at komme helt i mål med vores anstrengelser beregner vi afslutningvis den naturlige logaritme til hhv. venstresiden og højresiden, hvilket – idet \(\ln(e^x) = x\) – giver:
\(f’(x) = \frac{1}{x}, x>0\).
Vi har hermed vist, at differentialkvotienten for den naturlige logaritme \(f(x) = \ln(x), x>0\) er: \(f’(x) = \frac{1}{x}\). Det betyder, at overalt på grafen for den naturlige logaritme, se figur 2, kan vi beregne grafens hældning og dermed tangentens hældning som den reciprokke værdi af x.
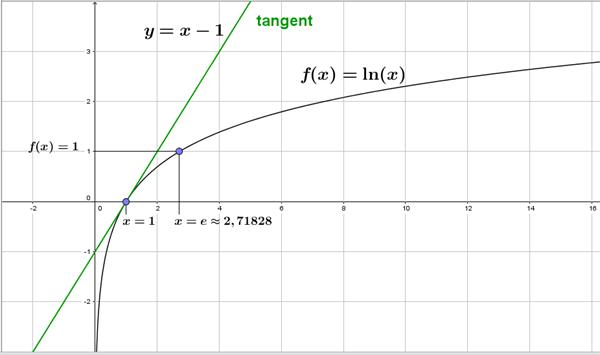
Figur 2 Grafen for \(f(x) = \ln(x)\)
I den forbindelse kan det særligt bemærkes, at i grafens skæringspunkt med x-aksen - punktet (1,0) - er tangentens hældning 1, og ligningen for denne tangent er derfor: \(y(x) = x - 1\), som er vist med grønt i figur 2.
