Andengradspolynomier
Typisk er andengradspolynomier (parabler) beskrevet ved en funktionsforskrift af typen:
\(f(x)=ax^2+bx+c\)
Selvom dette er en god måde, at skrive funktionsforskriften på, findes der også en anden udemærket måde, at gøre det på. Det er nemlig også muligt, at skrive et andengradspolynomium på formen:
\(f(x)=a(x-x_0)^2+y_0\)
Fordelen ved at beskrive et andengradspolynomium på formen \(f(x)=a(x-x_0)^2+y_0\) er, at vi kan aflæse toppunktet for funktionen direkte i funktionsforskriften. Toppunktet ligger nemlig i \((x_0, y_0)\). Vi kan derfor blot aflæse på funktionsforskriften.
Eksempel
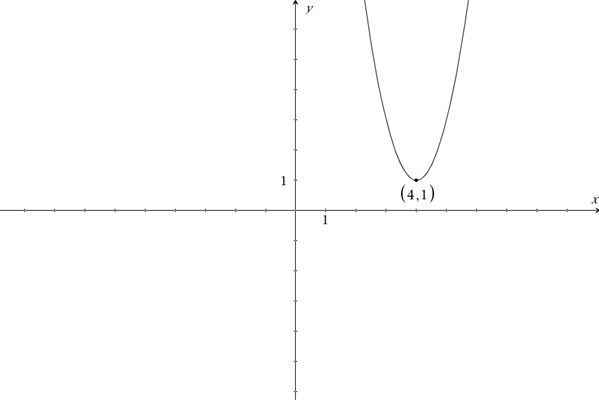
Vi har fået givet en funktion \(f(x)=2(x-4)^2+1\). I dette eksempel aflæser vi blot forskriften, og finder derved ud af, at toppunktet ligger i \((4,1)\). Man skal huske at tjekke fortegnet foran \(x_0\) og \(y_0\). Havde fortegnet foran vores \(x_0\)-værdi været positiv, ville vores \(x_0\) ikke være 4, men -4.
Et andet scenarie kunne være \(f(x)=2 \cdot x^2-16x+33\). I dette tilfælde kan vi ikke direkte aflæse toppunktet, da funktionen ikke står på formen \(f(x)=a(x-x_0)^2+y_0\). Vi kan derimod omskrive funktionsforskriften vha. kvadratsætningerne. Se eventuelt afsnit om kvadratsætningerne. Vi starter med vores oprindelige funktion:
\(f(x)=2 \cdot x^2-16x+33\)
Nu hvor vi benytter kvadratsætningerne, kunne det være interessant at se, om vi kunne omskrive sidste led til noget, der er lidt nemmere at arbejde videre med. Vi identificerer at: \(32=2 \cdot 4^2\). Vi skal blot huske, at lægge én mere til dette udtryk, så vi får 33:
\(f(x)=2 \cdot x^2-16x+2 \cdot 4^2+1\)
Vi kan nu faktorisere 2 ud for de første tre led:
\(f(x)=2 \cdot (x^2+4^2-8x)+1\)
Vi kigger nu på kvadratsætningerne, og vi ser at \(a^2+b^2-2ab=(a-b)^2\). Vi benytte nu denne information til, at omskrive funktionen:
\(f(x)=2 \cdot (x-4)^2+1\)
Ved at gøre dette, kommer vi frem til \(f(x)=2(x-4)^2+1\), altså nøjagtigt denne samme funktion som før. Denne gang var den blot skrevet på en anden form.På den måde kan man omskrive mellem de to måder at opskrive andengradspolynomiers funktionsforskrifter på.
