Logaritmiske skalaer: Introduktion

I et sædvanligt (x,y)-koordinatsystem er skalaen på hver af akserne lineær, dvs. overalt på hver af akserne svarer en bestemt afstand, f.eks. 1 cm, til en fast ændring i koordinaten. Skalaen (og enheden) på de to akser kan dog selvfølgelig være vidt forskellig – f.eks. kan x-aksen angive årstal og y-aksen angive mio. kr.

I nogle sammenhænge kan man med fordel ændre skalaen på den ene eller på begge akser til at være logaritmisk. Inden vi ser nærmere på nogle eksempler, må vi dog lige forstå, hvad en logaritmisk skala er.

Som logaritmisk skala benytter vi sædvanligvis logaritmen med grundtallet 10 (også kaldet 10-tals logaritmen og betegnet Log), da den giver nogle ”pæne” tal at se på og regne med. (Men vi kunne som logaritmisk skala principielt lige så godt benytte den naturlige logaritme (ln) med grundtallet \(e\) eller en logaritme-funktion med et vilkårligt andet grundtal.)

Som bekendt er Log(1) = 0, Log(10) = 1, Log(100) = 2, Log(1.000) = 3, osv. Vi kan introducere en logaritmisk skala på den positive del af y-aksen ved at lade heltallene 0, 1, 2, 3, osv. med samme afstand på aksen repræsentere y-værdierne hhv. 1, 10, 100, 1.000, osv.  Se figur 1a.

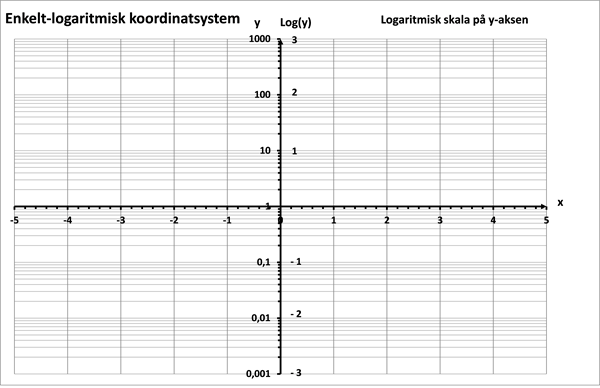
 Figur 1a         Enkelt-logaritmisk koordinatsystem med logaritmisk skala på y-aksen

En ændring på 1 på den logaritmiske skala giver altså en 10-dobling af y-værdien. Og afstanden på y-aksen mellem y = 1 og y = 10 er den samme som afstanden mellem y = 10 og y = 100 og afstanden mellem y = 100 og y = 1.000, osv. Jo længere vi bevæger os op ad y-aksen, desto grovere bliver skalaen.

På den negative del af y-aksen kan vi tilsvarende lade heltallene – 1, – 2, – 3 osv. med samme afstand på aksen repræsentere y-værdierne hhv. \(\frac{1}{10} = 0,1\), \(\frac{1}{100} = 0,01\), \(\frac{1}{1.000} = 0,001\), osv., idet Log(0,1) = – 1, Log(0,01) = – 2, Log(0,001) = – 3, osv. Jo længere vi bevæger os ned ad y-aksen, desto finere bliver skalaen.

På samme måde kan vi introducere en logaritmisk skala på x-aksen. Koordinatsystemet betegnes hhv. enkelt- og dobbelt-logaritmisk alt efter, om skalaen på kun den ene eller på begge akser er logaritmisk. I figur 1b er vist et dobbelt-logaritmisk koordinatsystem.

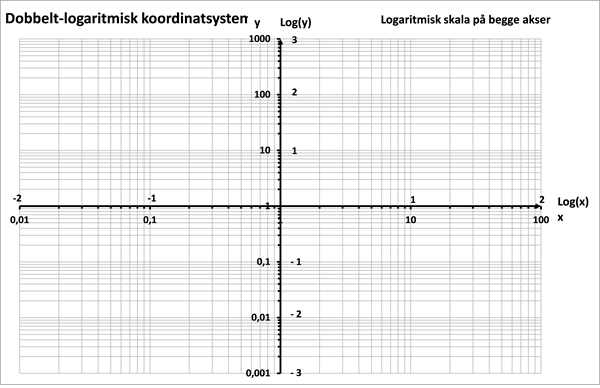
Figur 1b         Dobbelt-logaritmisk koordinatsystem med logaritmisk skala på både x-aksen og y-aksen

For at forstå anatomien i et logaritmisk koordinatsystem vil vi i det følgende se nærmere på, hvad der sker med punkter, når vi går fra  et sædvanligt (x,y)-koordinatsystem til et logaritmisk koordinatsystem. Vi taler om, at punkter og punktområder i det sædvanlige (x,y)-koordinatsystem ”spejles” til en ny position i det logaritmiske koordinatsystem.