Komposanter

Opdeling af komponenter:

Vi ved, at et punkt P kan opdeles i dens x- og y-komponenter: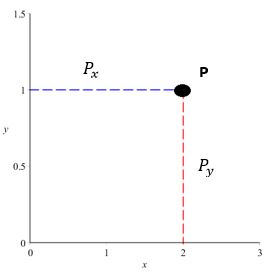

$$P=(P_x,P_y)$$  I dette eksempel har vi $$P=(2,1)$$

Vi kan bruge samme koncept med vektorer, hvor de også kan opdeles i x og y-dele. Hvis vi har en vektor a, kan vi opdele denne vektor i dens x- og y-komponenter:

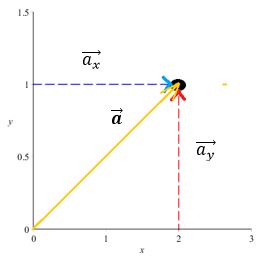og det skriver vi som $$\overrightarrow{a}=\overrightarrow{a_x}+\overrightarrow{a_y}$$ I vores eksempel har vi, at   $$\overrightarrow{a}=\begin{pmatrix}2\\0\end{pmatrix}+\begin{pmatrix}0\\1\end{pmatrix}=\begin{pmatrix}2\\1\end{pmatrix}\\$$

Længden af vektor ud fra komponenterne:

Hvis vi vil kende længden af en vektor a, og vi allerede kender dens komponenter, kan vi udregne længden med flg. formel:

$$\left|\overrightarrow{a}\right|=\sqrt{a_x^2+a_y^2}$$

Længder af komponenter:                                                                            

Ud fra enhedscirklen ved vi, at vi kan udtrykke koordinater $$(x,y)=(\cos(\theta),\sin(\theta))$$

Hvis vi kigger på vores opdeling af komposanter for vores vektor a, kan vi se, at det danner to retvinklede trekanter. Trekanternes sider er længderne af komposanterne (kateterne) og længden af vektoren a (hypotenusen):

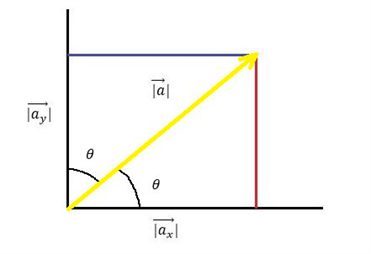
I en retvinklet trekant ved vi:

$$\cos(\theta)=\frac{hos}{hyp}=\frac{\left|\overrightarrow{a_x}\right|}{\left|\overrightarrow{a}\right|}$$

$$\rightarrow\left|\overrightarrow{a_x}\right|=\left|\overrightarrow{a}\right|\cdot\cos(\theta)$$

Og på samme måde fås:

$$\sin(\theta)=\frac{mod}{hyp}=\frac{\left|\overrightarrow{a_y}\right|}{\left|\overrightarrow{a}\right|}$$

$$\rightarrow\left|\overrightarrow{a_y}\right|=\left|\overrightarrow{a}\right|\cdot\sin(\theta)$$

Eksempel 1 - længden af en vektor ud fra komponenter

Vi har en vektor $$\overrightarrow{a}=\begin{pmatrix}6\\4\end{pmatrix}$$ og ud fra dens komposanter, vil vi gerne finde dens længde. $$\left|\overrightarrow{a}\right|=\sqrt{6^2+4^2}=\sqrt{36+16}=\sqrt{52}=7.21$$

Eksempel 2 - finde komposanter til en vektor ud fra længde og vinkel

Vi har en vektor a med længden 5, som danner en vinkel på 60 grader. Vi skal finde komponenterne til vektoren a.

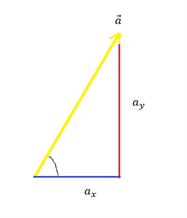
Vi finder først længderne af komposanterne:

$$\left|\overrightarrow{a_x}\right|=5\cdot\cos(60)=2.50$$

$$\left|\overrightarrow{a_y}\right|=5\cdot\sin(60)=4.33$$

Ud fra billedet kan vi se, at komponenterne kun har én koordinat hver som har en værdi, og vi har derfor komponenterne:

$$a_x=\begin{pmatrix}2.50\\0\end{pmatrix} \, \,  og \, \, \, a_y=\begin{pmatrix}0\\4.33\end{pmatrix}$$

Vi kan tjekke om vores resultat er rigtigt ved at indsætte de fundne størrelser ind i formlen:

$$\left|\overrightarrow{a}\right|=\sqrt{a_x^2+a_y^2}=\sqrt{(2.50)^2+(4.33)^2}=\sqrt{25}=5$$

Industrieksempel - Resulterende kraft og retningsændring på et fly

Et fly bliver ramt af et vindstød, som påvirker flyet med en kraft, så flyet skifter retning. Vi vil gerne finde den resulterende kraft F, og retningsændringen på flyet kaldet θ.

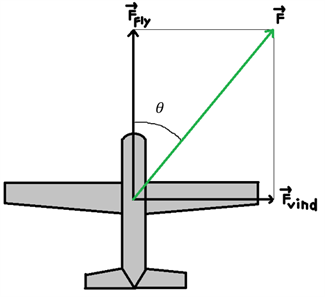
Ud fra figuren kan vi se, at den resulterende kraft F bliver beskrevet ved flyets fremdrift kaldet  F_fly og vindstødets kraft kaldet F_vind. Vi får oplyst, at de 2 komponenter har størrelserne: $$\left|\overrightarrow{F_{fly}}\right|=10000N \, \, \, og \, \, \,  \left|\overrightarrow{F_{vind}}\right|=8000N$$ 

Komposanterne har kun én værdi på enten x- eller y-delen, så vi kan opskrive komposanterne ud fra deres størrelser: $$\overrightarrow{F_{fly}}=\begin{pmatrix}0\\1\cdot10^4\end{pmatrix}N$$ $$\overrightarrow{F_{vind}}=\begin{pmatrix}8\cdot10^3\\0\end{pmatrix}N$$ Og den resulterende kraft kan findes ved at addere komposanterne: $$\overrightarrow{F}=\overrightarrow{F_{fly}}+\overrightarrow{F_{vind}}=\begin{pmatrix}0\\1\cdot10^4\end{pmatrix}N+\begin{pmatrix}8\cdot10^3\\0\end{pmatrix}N=\begin{pmatrix}8\cdot10^3\\1\cdot10^4\end{pmatrix}N$$ Vi kan nu finde størrelsen af den resulterende kraft. $$\left|\overrightarrow{F}\right|=\sqrt{F_{fly}^2+F_{vind}^2}=\sqrt{(1\cdot10^4N)^2+(8\cdot10^3N)^2}=1.28\cdot10^4N$$

Herfra kan vi finde retningsændringen af flyet.

$$\sin(\theta)=\frac{mod}{hyp}=\frac{\left|\overrightarrow{F_{vind}}\right|}{\left|\overrightarrow{F}\right|}$$ $$\implies \sin(\theta)=\frac{8\cdot10^3N}{1.28\cdot10^4N}=0.625$$ $$\implies \theta=38.68^ {\circ}$$