Trekantens areal (ud fra vinkel mellem vektorer)

Areal af trekant ("appelsin-formlen"):

Vi skal prøve at finde et udtryk, hvor vi relaterer vores viden om vektorregning til de arealformler, vi allerede kender. Vi vil derfor gerne kunne udlede en formel, som vi kan sammenholde den med den mest almindelige arealformel for trekanter: $$T=\frac{1}{2}hg$$

Vi kan kigge på en situation, hvor vi kan prøve at finde et udtryk for grundlinjen g og højden h:  

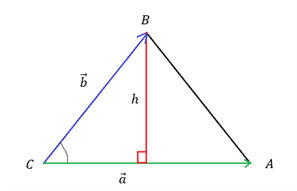Ud fra vores viden om retvinklede trekanter, kan vi opskrive $$\sin(C)=\frac{mod}{hyp}=\frac{h}{\left|\overrightarrow{b}\right|} $$ $$\implies h ={\left|\overrightarrow{b}\right|}\cdot sin(C)$$ Grundlinjen g er lig længden af vektor a, som vist på tegningen. Derfor kan vi nu indsætte vores udtryk for højden h og grundlinjen g i arealformlen og få et nyt udtryk: $$T=\frac{1}{2}{\left|\overrightarrow{a}\right|}\cdot{\left|\overrightarrow{b}\right|}\cdot \sin(C)$$ Denne formel kan relateres til "appelsinformlen", som er givet ved $$T=\frac{1}{2}a\cdot b\cdot \sin(C)$$

Areal af trekant (krydsprodukt):

Vi kan omskrive vores formel yderligere, da vi ved, at krydsproduktet er givet ved $${\left|\overrightarrow{a}\right|}\cdot{\left|\overrightarrow{b}\right|}\cdot sin(C)={\left|\overrightarrow{a}\times\overrightarrow{b}\right|}$$ Så vi kan også skrive vores arealformel som $$T=\frac{1}{2}{\left|\overrightarrow{a}\right|}\cdot{\left|\overrightarrow{b}\right|}\cdot sin(C)=\frac{1}{2}{\left|\overrightarrow{a}\times\overrightarrow{b}\right|}$$

 Eksempel 1 - find areal af en trekant ud fra to givne vektorer:

Vi har fået oplyst vektorerne a og b: $$\overrightarrow{a}=\begin{pmatrix}4\\3\end{pmatrix} \, \, og \, \, \,  \overrightarrow{b}=\begin{pmatrix}2\\-5\end{pmatrix}$$ De to vektorer danner en trekant med en tredje vektor C:

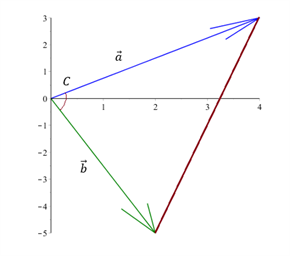
Vi ønsker at udregne arealet af denne trekant:

Vinklen C skal først findes, og det kan vi gøre ved hjælp af skalarproduktet. $$\cos(C)=\frac{a_xb_x+a_yb_y}{\left|\overrightarrow{a}\right|\cdot\left|\overrightarrow{b}\right|}=\frac{4\cdot2+3\cdot(-5)}{\sqrt{4^2+3^2}\sqrt{2^2+(-5)^2}}=-0.26$$ $$\implies C=105^\circ$$ Nu kan vi indsætte i arealformlen $$T=\frac{1}{2}{\left|\overrightarrow{a}\right|}\cdot{\left|\overrightarrow{b}\right|}\cdot \sin(C)=\frac{1}{2}\cdot5\cdot\sqrt{2^2+(-5)^2}\cdot \sin(105)=13$$

Eksempel 2 - finde en vinkel ud fra arealformlen:

Arealet af trekanten er 20, længden af vektor a er 7 og vektor b er givet ved $$\overrightarrow{b}=\begin{pmatrix}15\\9\end{pmatrix}$$

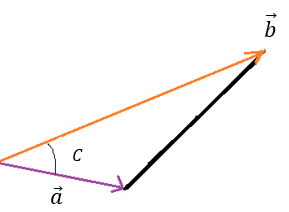
Vi skal finde vinklen C imellem de to vektorer: $$T=\frac{1}{2}\left|\overrightarrow{a}\right|\cdot\left|\overrightarrow{b}\right|\cdot \sin(C)\implies \sin(C)=\frac{2T}{\overrightarrow{\left|a\right|}\cdot\overrightarrow{\left|b\right|}}$$ $$\sin(C)=\frac{2\cdot 20}{7\cdot\sqrt{15^2+9^2}}=0.326$$ $$\implies C=19^\circ$$

Eksempel 3 - beregn areal ud fra størrelsen (den numeriske værdi) af krydsproduktet:                                            

Vi skal finde arealet ud fra krydsproduktet. Vektorerne er givet ved $$\overrightarrow{a}=\begin{pmatrix}1\\7\end{pmatrix} \, \, og \, \, \, \overrightarrow{b}=\begin{pmatrix}-6\\5\end{pmatrix}$$

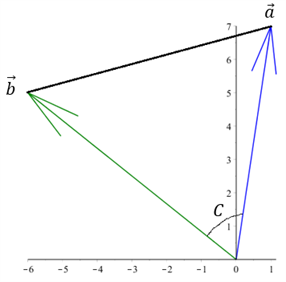
Da vi skal bruge krydsproduktet i denne opgave, anvender vi formlen: $$T=\frac{1}{2}{\left|\overrightarrow{a}\times\overrightarrow{b}\right|}=\frac{1}{2}(a_xb_y-a_yb_x)$$ $$T=\frac{1}{2}(1\cdot5-7\cdot(-6))=23.5$$

Industrieksempel - Find areal af en trekant dannet ud fra laseropmåling:

Laseropmåling bliver normalt brugt til at bestemme længde og bredde af et firkantet rum. Denne situation er nem at udregne, da det kun kræver at man ganger den fundne længde og bredde sammen (som vi kan betragte som vektorer), som vist i følgende situation: 

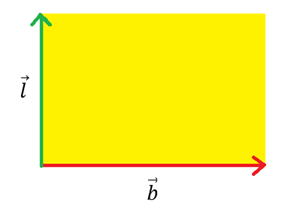
Det gule område er arealet, som man kan udregne ved at gange størrelsen af de 2 vektorer sammen.  $$A={\left|\overrightarrow{l}\right|}\cdot{\left|\overrightarrow{b}\right|}$$ Men vi kan også sagtens forestille os en situation, hvor vi ønsker at finde arealet af en trekant i stedet for en firkant. Vi bruger laseropmåleren igen og kalder de to retninger, som vi måler på for r₁ og r₂:

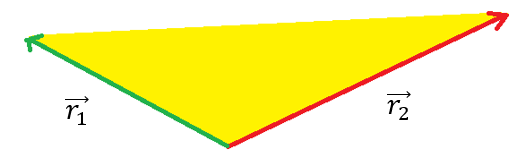
Vi ønsker at finde det gule område, som er vores areal. Vi kan forestille os, at vi har designet laseropmåleren til at kunne udregne de to retningsvektorer, så får vi opgivet de to retningsvektorer r₁ og r₂: $$\overrightarrow{r_1}=\begin{pmatrix}-5\\10\end{pmatrix}m \, \, \, og \, \, \, \overrightarrow{r_2}=\begin{pmatrix}6\\12\end{pmatrix}m$$ Arealet af trekanten udregnes ved krydsproduktsformlen $$T=\frac{1}{2}{\left|\overrightarrow{r_1}\times\overrightarrow{r_2}\right|}=\frac{1}{2}(a_xb_y-a_yb_x)$$ $$\rightarrow T=\frac{1}{2}{\left|(-5m)\cdot(12m)-(10m)\cdot(6m)\right|}=\frac{1}{2}{\left|-120 \, m^2\right|}=60 \, m^2$$