Enhedsvektor

Hvad er en enhedsvektor?  

Vi kan have et specialtilfælde hvor længden af en vektor er 1, dvs. $$\left|\overrightarrow{a}\right|=\sqrt{a_x^2+a_y^2}=1$$ Vi kalder denne specielle vektor med længden 1 for en enhedsvektor. Dvs. en enhedsvektor er givet ved: $$\left|\overrightarrow{e}\right|=1$$

Enhedsvektorer kan have forskellige retninger, men altid samme længde. Her er eksempler på nogle enhedsvektorer:

$$\overrightarrow{e_1}=\begin{pmatrix}0.707\\0.707\end{pmatrix} \, , \,  \overrightarrow{e_2}=\begin{pmatrix}-0.632\\0.774\end{pmatrix} \,  , \,  \overrightarrow{e_3}=\begin{pmatrix}0.500\\-0.866\end{pmatrix} \, \, og \, \, \overrightarrow{e_5}=\begin{pmatrix}-0.948\\-0.316\end{pmatrix}$$

Vi kan tjekke længden af en af enhedsvektorerne for at se, om den nu også har længden 1: $$\overrightarrow{e_2}=\sqrt{(-0.632)^2+(0.774)^2}=\sqrt{0.4+0.6}=\sqrt{1}=1$$

Vi kan illustrere enhedsvektorerne i et koordinatsystem og indsætte enhedscirklen i det samme koordinatsystem: 

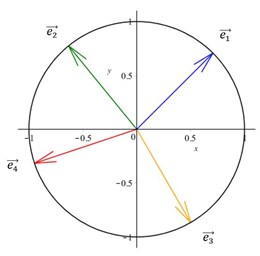
Vi kan se, at alle enhedsvektorerne berører enhedscirklen. Dette giver også god mening, da en enhedsvektor svarer til radius på enhedscirklen (og begge har størrelsen 1). 

Lav en vilkårlig vektor om til en enhedsvektor:

Vi ønsker at finde et udtryk, hvor vi kan lave en vektor om til en enhedsvektor. Komponenterne til enhedsvektoren finder vi ved at tage forholdet mellem den ønskede enhedsvektor og vektoren, som vi ønsker at lave til enhedsvektor. $$\frac{e_x}{a_x}=\frac{\left|\overrightarrow{e}\right|}{\left|\overrightarrow{a}\right|}=\frac{1}{\left|\overrightarrow{a}\right|}$$ $$\implies  e_x=\frac{a_x}{\left|\overrightarrow{a}\right|}=\hat{a_x}$$ y-komponenten findes på samme måde,$$\implies  e_y=\frac{a_y}{\left|\overrightarrow{a}\right|}=\hat{a_y}$$ Vi kan nu opskrive komponenterne som et samlet udtryk $$\overrightarrow{e}=\begin{pmatrix}e_x\\e_y\end{pmatrix}=\begin{pmatrix}\frac{a_x}{\left|\overrightarrow{a}\right|}\\\frac{a_y}{\left|\overrightarrow{a}\right|}\end{pmatrix}=\frac{\begin{pmatrix}a_x\\a_y\end{pmatrix}}{\left|\overrightarrow{a}\right|}=\frac{\overrightarrow{a}}{\left|\overrightarrow{a}\right|}$$ Dvs. at man kan omskrive en vektor til en enhedsvektor med formlen $$\overrightarrow{e}=\frac{\overrightarrow{a}}{\left|\overrightarrow{a}\right|}=\hat{a}$$

(Standard) basisvektorer:                                                      

Vi kan have specielle enhedsvektorer, som vi betegner som basisvektorerne. $$\hat{\imath}=\begin{pmatrix}1\\0\end{pmatrix}$$$$\hat{\jmath}=\begin{pmatrix}0\\1\end{pmatrix}$$ Med disse to enhedsvektorer kan vi udtrykke enhver vilkårlig vektor.

$$\overrightarrow{a}=\begin{pmatrix}a_x\\a_y\end{pmatrix}=a_x\cdot\begin{pmatrix}1\\0\end{pmatrix}+a_y\cdot\begin{pmatrix}0\\1\end{pmatrix}=a_x\cdot\hat{\imath}+a_y\cdot\hat{\jmath}$$

Eksempel 1 - tjek, om tilfældig vektor er en enhedsvektor

Vi skal tjekke om vektor a er en enhedsvektor. Denne vektor er givet ved $$\overrightarrow{a}=\begin{pmatrix}0.3\\0.7\end{pmatrix}$$ Vi skal udregne, om længden af vektoren er 1.  $$\left|\overrightarrow{a}\right|=\sqrt{0.3^2+0.7^2}=\sqrt{0.58}=0.76$$

Vektoren er altså ikke en enhedsvektor, da den ikke har længden 1.

Dette kan vi også se i forhold til vores viden omkring enhedsvektorer og enhedscirklen: 

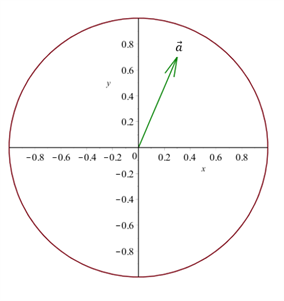
Eksempel 2 - lav en tilfældig vektor om til en enhedsvektor

Vi har en vektor \(\overrightarrow{a}=\begin{pmatrix}4\\4\end{pmatrix}\) , som vi skal lave til en enhedsvektor.                                                                                  

Vi skal finde længden af vektoren, så vi kan beregne enhedsvektoren. $$\left|\overrightarrow{a}\right|=\sqrt{4^2+4^2}=\sqrt{32}=5.657$$Nu kan vi bare indsætte i vores formel og få $$\hat{a}=\frac{\begin{pmatrix}4\\4\end{pmatrix}}{5.657}=\begin{pmatrix}\frac{4}{5.657}\\\frac{4}{5.657}\end{pmatrix}=\begin{pmatrix}0.707\\0.707\end{pmatrix}$$

Hermed har vi lavet vores vektor om til en enhedsvektor.

Eksempel 3 - udtryk en tilfældig vektor med (standard) basisvektorer

Vi har en vektor givet ved $$\overrightarrow{a}=\begin{pmatrix}5\\7\end{pmatrix}$$  Vi ønsker at udtrykke denne vektor ved hjælp af (standard) basisvektorer. $$\overrightarrow{a}=5\cdot\begin{pmatrix}1\\0\end{pmatrix}+7\cdot\begin{pmatrix}0\\1\end{pmatrix}=5\cdot\hat{\imath}+7\cdot\hat{\jmath}$$ 

Industrieksempel - En satellits enhedsvektor og gravitationslov

En satellit er i kredsløb om jorden, og vi ved fra den universelle gravitationslov, at kraften mellem to objekter er givet ved $$F=G\cdot\frac{m_1m_2}{r^2}$$I denne formel er G den universelle gravitationskonstant. Vi er interesseret i at finde størrelsen af denne kraft F og dens retning.

Vi har en situation, hvor satelliten vejer 150 kg og afstanden mellem satelliten og jorden er 35800 km. Vi ved desuden at jordens masse er ca. 6·10²⁴ kg. 

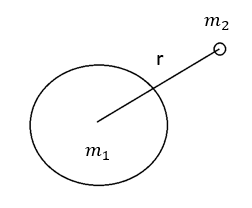
Vi kan starte med at finde størrelsen af kraften F, dvs. vi indsætter de oplyste værdier i den universelle gravitationslov: $$F=G\cdot\frac{6\cdot10^{24}kg\cdot150kg}{(3.58\cdot 10^7m)^2}=G(7\cdot10^{11}\frac{(kg)^2}{m^2})$$ Her kan vi indsætte værdien for konstanten G: $$\implies F= 6.7\cdot10^{-11}\frac{Nm^2}{(kg)^2}\cdot(7\cdot10^{11}\frac{(kg)^2}{m^2})=47N$$

Vi kan opfatte denne afstand r som en retningsvektor, og vi kan beskrive situationen med en vektor. Hvis vi også får oplyst vektor r's komponenter, kan vi nu få: 

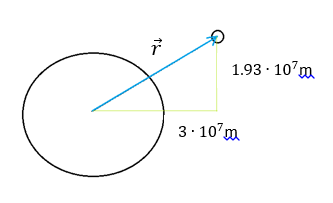Dvs. vi har nu en retningsvektor givet ved $$\overrightarrow{r}=\begin{pmatrix}3\\1.93\end{pmatrix}\cdot10^7m$$ Vi skal nu finde en måde at få beskrevet retningen af F, da vi lige har regnet størrelsen ud. Hvis vi benytter viden fra f.eks. projektion, hvor vi kan komme frem til formlen $$\overrightarrow{b}_{\overrightarrow{a}}=\left|\overrightarrow{b_{\overrightarrow{a}}}\right|\cdot\hat{a},$$  hvor vi kan se, at en vektor kan udtrykkes som størrelsen af vektoren ganget med en enhedsvektor for at angive retningen.        

Dette kan vi benytte til at opskrive en formel for at angive retningen af kraften F: $$\overrightarrow{F}=\left|\overrightarrow{F}\right|\cdot\hat{r}$$

Vi er nødt til at bruge en enhedsvektor i stedet for en almindelig retningsvektor, da vi ellers ville få både forkerte enheder og forkert størrelse på vores resultat. Vi kan vise dette ved at prøve at udregne retningen af kraften ved brug af retningsvektoren r, som er en FORKERT METODE!  $$ \overrightarrow{F}\neq\left|\overrightarrow{F}\right|\cdot\overrightarrow{r}$$$$\implies \overrightarrow{F}\neq47N\cdot\begin{pmatrix}3\\1.93\end{pmatrix}\cdot10^7m=\begin{pmatrix}1.41\\9.01\end{pmatrix}\cdot10^9Nm$$ og hvis vi prøver at omregne størrelsen tilbage igen burde vi selvfølgelig få det samme (dvs. 47N), men i stedet får vi: $$\left|\overrightarrow{F}\right|\neq\sqrt{(1.41\cdot10^9Nm)^2+(9.01\cdot10^9Nm)^2}=9.18\cdot10^9Nm$$ Derfor SKAL vi vi benytte formlen med enhedsvektor! Vi skal derfor omregne retningsvektoren til en enhedsvektor: $$\hat{r}=\frac{\overrightarrow{r}}{\left|\overrightarrow{r}\right|}\implies\hat{r}=\frac{\begin{pmatrix}3\\1.93\end{pmatrix}\cdot10^7m}{3.58\cdot10^7m}=\begin{pmatrix}\frac{3}{3.58}\\\frac{1.93}{3.58}\end{pmatrix}=\begin{pmatrix}0.84\\0.54\end{pmatrix}$$ Vi kan nu endelig udregne retningen af kraften F $$\overrightarrow{F}=47N\cdot\begin{pmatrix}0.84\\0.54\end{pmatrix}=\begin{pmatrix}39.5\\25.4\end{pmatrix}N$$