At afsætte en vinkel på 60°

Der er givet en linje (\(l\)) og et punkt (\(A\)) på linjen, som vist med blåt på figuren. Vi skal afsætte en 60° vinkel i punkt \(A\), dvs. konstruere en linje (\(m\)), som danner vinklen 60° med linjen \(l\) og går gennem punkt \(A\). 

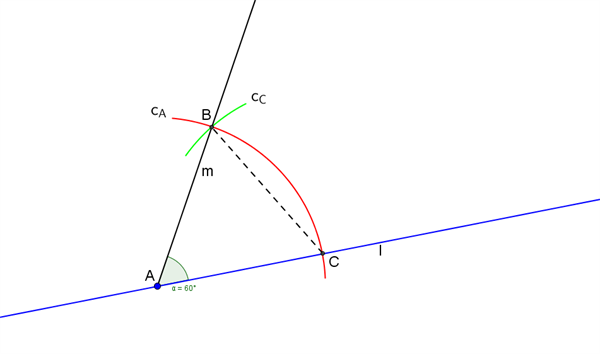
Figur          At afsætte en vinkel på 60°

Fremgangsmåde, se figuren:

1. tegn – med centrum i punkt \(A\) – en cirkel (\(c_A\)) med en selvvalgt radius, og bevar radius på din passer (på figuren er kun vist den cirkelbue (rød) hørende til cirklen \(c_A\), som forløber fra skæring med linjen \(l\) op til lidt mere end 60° over linjen \(l\) set fra punkt \(A\))
2. skæringspunktet mellem cirkelbuen hørende til cirklen \(c_A\) og linjen \(l\) betegnes \(C\)  
3. tegn – med centrum i punkt \(C\) – en cirkel (\(c_C\)) med samme radius som i cirkel \(c_A\) (på figuren er kun vist den cirkelbue (grøn) hørende til cirklen \(c_C\), som skærer cirkelbuen hørende til cirklen \(c_A\))
4. skæringspunktet mellem cirkelbuerne hørende til cirklerne \(c_A\) og \(c_C\) betegnes \(B\)
5. vinkel \(\angle BAC\) er 60°, og halvlinjen (\(m\)) fra punkt \(A\) gennem punkt \(B\) er dermed den ønskede linje, som danner vinklen 60° med linjen \(l\) og går gennem punkt \(A\)

Trekant \(ABC\) er i øvrigt en regulær (dvs. ligesidet og ligevinklet) trekant, hvor vinklerne \(\angle ACB\) og \(\angle CBA\) også er 60°.