Eksempel trekant
Arealet af en trekant er givet ved formlen:
\(A_{trekant}=\frac{1}{2}h\cdot g\)
hvor g er grundlinjen, og h er højden. Længden g er defineret som længden fra A til B. Højden h er så defineret som distancen fra C, vinkelret ned på g. Så længe vi bruger denne definition, så kan vi altid finde et korrekt areal, uanset om trekanten er retvinklet, som i figur 4A, eller ikke, som i figur 4B.
Forestil, at vi har en rektangulær væg. Væggens areal findes som
\(A = h\cdot g\)
som påvist i afsnittet om rektangler. Vi skærer så væggen midt over på diagonalen, som vist på tegningen.
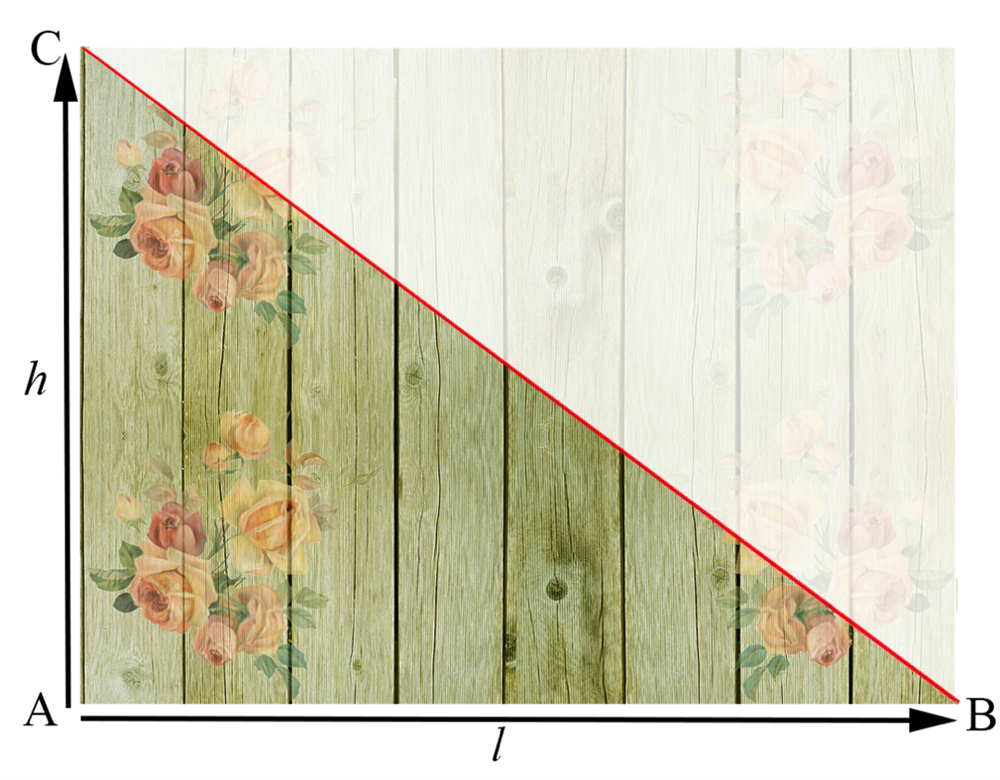
Nu har vi altså to retvinklede trekanter, der begge er lige store. Fordi summen af trekanternes arealer tilsammen giver arealet af vores tidligere flise, så må hver trekant have et areal på halvdelen af flisens areal, dvs.,
\(A_{trekant}=\frac{1}{2}h\cdot g\)
Men hvad hvis trekanten ikke er retvinklet? Tja, det viser sig, at det ingen forskel gør, så længe vi bruger den anviste metode til at finde h og g. Beviset er dog lidt mere kompliceret, så hvis man ikke finder den slags interessant, så kommer her en nem huskeregel til alle trekanters areal:
En trekant med grundlinje \(g\) og højde \(h\) fylder kun halvdelen af rektanglet med samme længde og højde. Derfor er arealet af trekanten halvdelen af rektanglet.

