Rampens vinkel
Sinusrelationer
Når man arbejder med geometri, så er det ofte vigtigt at kunne regne med vinkler. Det kan være man skal bygge en konstruktion som skal have en specifik vinkel for at den passer korrekt ind. Der skal fremstilles en retvinklet trekant, hvor kateterne skal være 45cm og 75cm. Vi skal bestemme en af vinklerne i trekanten, da et andet element skal skæres til efter den vinkel.
Ved hjælp af Pythagoras kan vi nemt finde længden på hypotenusen.
$$ 45^2+75^2=7650 \Longrightarrow \sqrt{7650}=87.46$$
Vi kender alle sidelængder i trekanten, og vi kender én vinkel, nemlig den på 90°. Med de informationer kan vi bestemme de to sidste vinkler. Til det skal vi bruge sinusrelationerne,
$$\frac{a}{sin(A)}=\frac{b}{sin(B)}=\frac{c}{sin(C)}$$
eller
$$\frac{sin(A)}{a}=\frac{sin(B)}{b}=\frac{sin(C)}{c}$$
Hvilken en af de to ovenstående man bruger, afhænger af om det er vinkler eller sidelængder man ønsker at finde. Vi er ude efter vinkler, så vi skal bruge \(\frac{sin(A)}{a}=\frac{sin(B)}{b}=\frac{sin(C)}{c}\).
Vores trekant kan vi tegne sådan her:
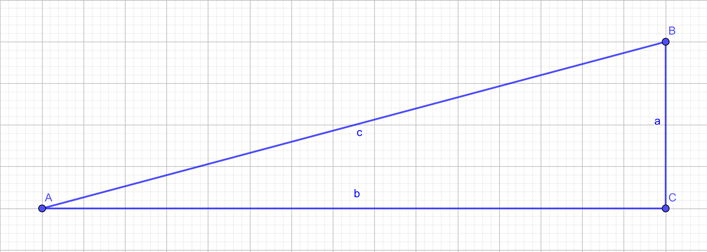
Alt skrevet med store bogstaver er vinkler og små bogstaver er sidelængder. Vi kender følgende:
a = 45cm
b = 75cm
c = 87.46cm
C = 90°
Vi vil gerne finde vinkel B. Vi indsætter tal i sinusrelationerne
$$\frac{sin(90°)}{87.46cm}=\frac{sin(B)}{75cm}$$
Vi ganger med 75cm på begge sider af lighedstegnet for at isolere \(sin(B)\).
$$\frac{sin(90\textdegree)}{87.46cm}\cdot 75cm=0.8575348730848389$$
Vores vinkel er ikke \(0.8575348730848389\), tallet er nemlig sinus til vinkel B. For at finde vinklen i grader, så skal vi bruge \(arcsin\) funktionen.
$$arcsin(0.8575348730848389) = 59.04°$$
Nu har vi bestemt vinkel B. Eksemplet her er for en retvinklet trekant, men det smarte ved sinusrelationerne er, at de kan benytte i en vilkårlig trekant. Man behøver altså ikke have en ret vinkel.
