Cosinus og sinus
Enhedscirklen
Indenfor trigonometrien benytter man en særlig cirkel kaldet enhedscirklen. Det særlige ved den er, at den har centrum i origo (dvs. punktet (0, 0)), og har radius 1.

Enhedscirklen er vigtig, fordi det er ud fra den, vi definerer funktionerne cosinus og sinus.
Cosinus og Sinus
Cosinus og Sinus er to funktioner, hvor man putter en vinkel ind, og hvor der så kommer et tal mellem -1 og 1 ud. De kaldes trigonometriske funktioner, fordi man kan bruge dem til at beregne ting, der har med trekanter at gøre.
Men hvad er de egentlig for nogle funktioner? Hvis du vil se et eksempel på, hvor cosinus og sinus kan bruges i virkeligheden, kan du klikke her.
Mens mange funktioner er givet direkte ved en forskrift, er cosinus og sinus givet ud fra enhedscirklen.
Lad os kalde den vinkel, vi ønsker at putte ind i cosinus eller sinus, for v. Nu indtegner vi vinkel v i samme koordinatsystem som en enhedscirkel. Vi placerer v, så den har toppunkt i origo og har sit højre vinkelben langs x-aksen. Det venstre vinkelben vil skære enhedscirklen i et punkt, som vi kalder Pv, retningspunktet.
Koordinat-sættet til Pv er simpelthen cos(v) og sin(v), således at x-koordinaten er cos(v) og y-koordinaten er sin(v).
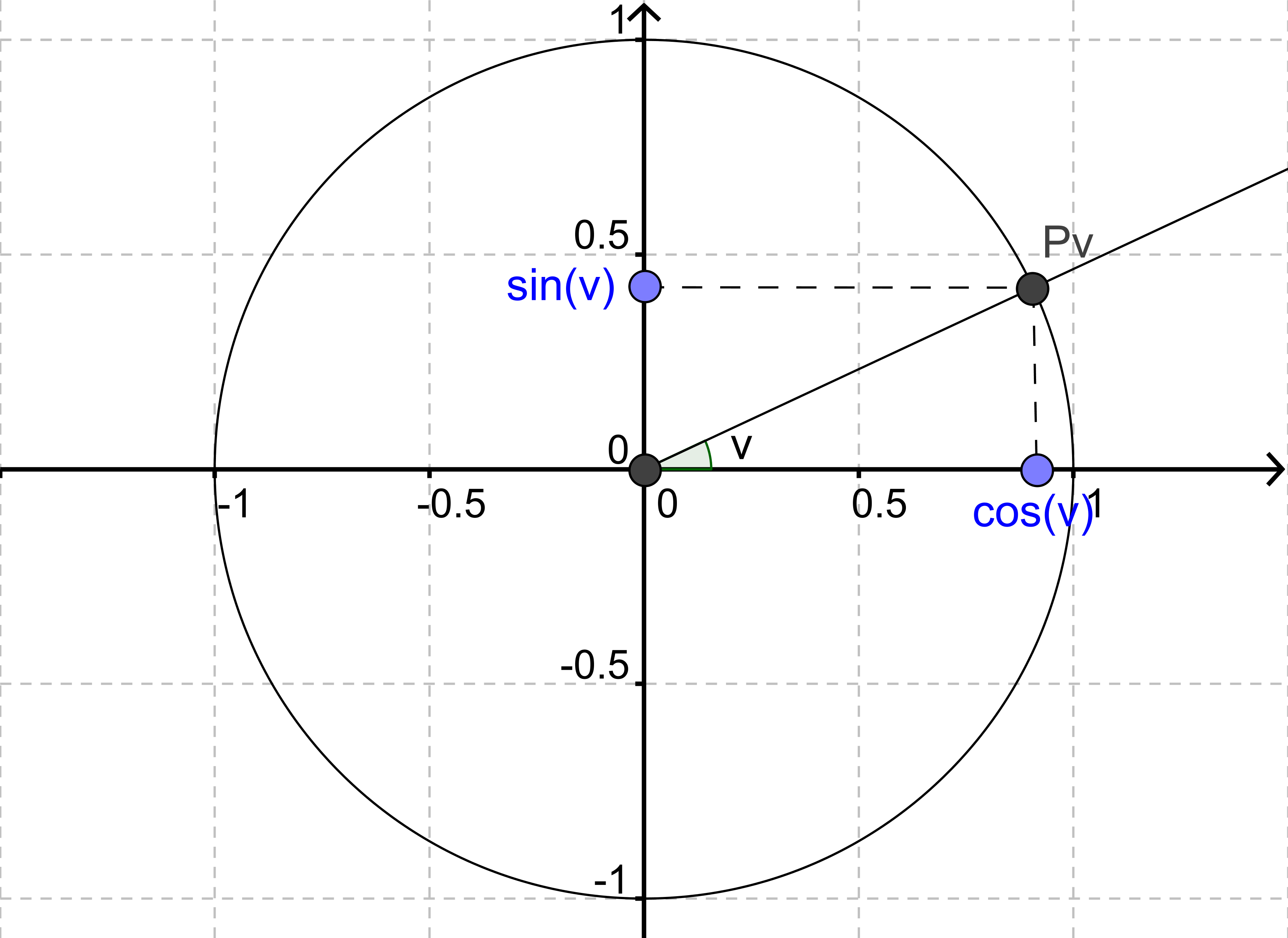
Så hvis du bliver spurgt, hvad sinus og cosinus er, kan du svare, at det simpelthen bare er koordinatsættet til et punkt på enhedscirkelen.
Lad os prøve at indtegne en vinkel på 35º
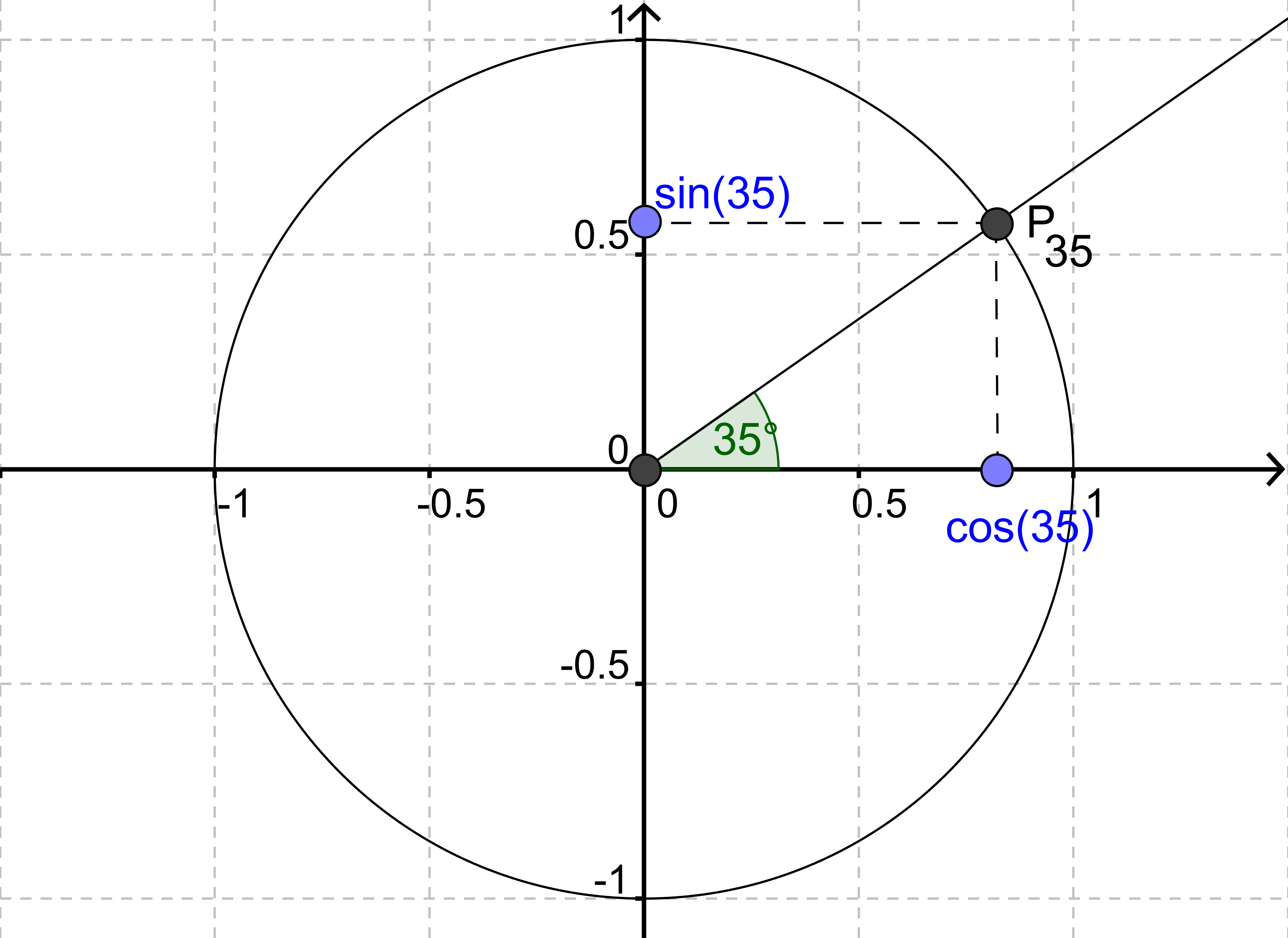
Hvis man kunne aflæse meget præcist, kunne man se at
$$P_{35}(0.819,\,0.574)$$
hvilket betyder at
$$\cos(35^\circ)=0,819$$
$$\sin(35^\circ)=0,574$$
Der er ingen, der kan aflæse så præcist. Så i praksis benytter man en lommeregner, der har indbygget knapper for cosinus og sinus.
Her er en tabel med nogle af de vigtige værdier for cosinus og sinus.
| Vinkel | Cosinus | Sinus |
| 0° | 1 | 0 |
| 30° | 0,866 | 0,5 |
| 45° | 0,707 | 0,707 |
| 60° | 0,5 | 0,866 |
| 90° | 0 | 1 |
| 120° | -0,5 | 0,866 |
| 135° | -0,707 | 0,707 |
| 150° | -0,866 | 0,5 |
| 180° | -1 | 0 |
| 210° | -0,866 | -0,5 |
| 225° | -0,707 | -0,707 |
| 240° | -0,35 | -0,866 |
| 270° | 0 | -1 |
| 300° | 0,5 | -0,866 |
| 315° | 0,707 | -0,707 |
| 330° | 0,866 | -0,5 |
| 360° | 1 | 0 |
cos-1 og sin-1
Det er også muligt at regne den anden vej. Hvis man har et tal mellem -1 og 1 og vil vide, hvilken vinkel det er sinus- (eller cosinus-)værdi for, så kan man bruge funktionerne sin-1 eller cos-1 (som også findes på lommeregneren).
Hvis vores tal f.eks. er 0,574, og vi vil finde ud af hvilken vinkel, v, det er cosinus for, kan vi gøre således.
$$
\begin{align}
\cos(v) &= 0,574 \Leftrightarrow\\
v &=\cos^{-1}(0,574) \\
v &=54,97^\circ
\end{align}$$
En anden måde at forklare det på er, at hvis man vil rykke cos hen på den anden side af lighedstegnet, så bliver det til cos-1. Præcis ligesom plus bliver til minus, og gange til dividere, når man rykker det over lighedstegnet.
